Handling NULL values in Preference SQL
Introduction
In SQL NULL values model incomplete or unknown data and are thus an important concept in order to be consistent with the real world in practice. In SQL the handling of NULL values led to an ongoing controversy discussion which in the end resulted in the nowadays applied three-valued logic consisting of true, false and the value unknown. Hence, comparisons with NULL values never lead to true or false, but to the third logical value unknown.
NULL values in preference database queries are still an open topic of research. Until now most of the preference query approches and its algorithms rely on the assumptions of transitivity in the preference order and the absence of NULL values in the data, i.e. all dimensions are available for all tuples. The first assumptions of dominance transitivity is mainly used to speed up the query processing algorithms by applying indexes and pruning to the used data structures. But obviously the second assumption does not hold for the real world in practice, where NULL values in sense of incomplete or unknown data occur every day.
Consider the case of a social online plattform for hiking tours, where everybody can add and describe a new hiking tour. It is highly unlikely that a user can or wants to provide all the possible information about a hiking tour. The following table illustrates a small and simple database relation containing hiking tour data:
| id | length | difficulty | rating | vista |
| 1 | 23.5 | medium | 4 | excellent |
| 2 | NULL | easy | 5 | bad |
| 3 | NULL | NULL | 2 | bad |
| 4 | 13.1 | hard | 2 | good |
| 5 | 7.3 | NULL | 1 | excellent |
Now the question is, how should one compare the unknown NULL values to the known values in a preference database query. For example, if a user wants to find tours with a length of around 20 kilometers, how are the values 7.3, 13.1 and 23.5 compared to NULL?
Cautious and accurate users perhaps want to see NULL values rated worse than any other available value, whereas adventurous users maybe would like to see the tours with NULL values in the length attribute among the best available offers. The way to handle NULL values in Preference SQL provides more versatile options as the subsequent remarks will reveal.
The following sections present the approach to handle NULL values which is used in Preference SQL. This one preserves the desired transitivity relation and the assumption of data completeness is not necessary anymore.
NULL values in preference algebra
The next passage formally defines the handling of NULL values in preferences as applied in Preference SQL NULL-extension.
NULL-extended attribute domain
In the approach taken by Preference SQL, NULL is fully integrated into the preference order, i.e. NULL is comparable to any other value of the domain. Formally the NULL-extended domain is defined by
dom_N(A) := dom(A) ∪ {NULL}
In standard SQL a comparison with a NULL value always results in a third logic value called unknown. The approach taken in Preference SQL uses the two-valued boolean logic with true and false, i.e. an expression x <_P NULL or NULL <_P x with x ∈ dom_N(A) is either true or false. Additionally it is required that the NULL-extended preference relation <_P is transitive.
One possibility to extend preferences to the NULL-extended domain is to treat NULL values as values of the original attribute domain, i.e. NULL is inserted into the preference order at the same place as values from the original domain. Hence, for categorical preferences, NULL can be be part of one of the layer or we can assign a certain level to NULL values. For numerical preferences is is possible to define a level or distance to the optimal values, which makes NULL values equivalent to other ordinary attribute values. Moreover for both types of base preferences exists the possibility to avoid NULL values, i.e. make them least preferred or place them among the worst available attribute values.
Another approach to treat NULL values in preferences is to make them incomparable to all other attribute values, i.e. the expression x <_P NULL is false for all x. This represents the missing information character of NULL values. If specified to be incomparable, NULL values do not dominate any other value and are not dominated by any other value, thus they always occur in the preference's BMO-set.
NULL-extended categorical preference constructors
For categorical preference constructors the first option is to use NULL values as usual domain values in one of the layers. Taking the hiking tour example from above, NULL can be placed in any layer of a LAYERED-preference on the attribute difficulty, e.g.
LAYERED(difficulty,({easy},{medium},{hard,NULL},OTHERS))
In this example, hiking tours with a difficulty of hard are rated equally good as the ones for which the attribute is NULL. To specify that NULL values are incomparable to all other values, to place them among the worst values or to avoid them, i.e. make them least preferred, a NULL-handling parameter N is introduced for the categorical preference constructors. Formally let
P = C(A,X,≅_P)
be a categorial preference with a preference constructor C on an attribute A, parameters X (layers, POS-set, NEG-set, etc.) and a SV-relation, hence, we define
P‘ = C(A,X,≅_P,N)
to be the same categorical preference plus the additional NULL-handling parameter. The parameter N may take one of the following values:
- N_? means that NULL values are incomparable to all other values and thus leads to a preference order <p‘ given by
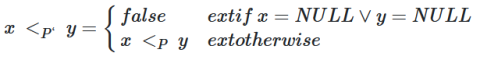
Keep in mind that if NULL is incomparable, the categorical base preference is not a weak order anymore.
- N_v places NULL values at the level v of the categorical preference. Thereby the value v can take on two extreme values:
- N_max sets the score for NULL to the maximum available score value, i.e. undefined
- N_∞ makes NULL values least preferred, i.e. they are only considered in case there is nothing better available than NULL values. Formally the preference's score function is set to infinity: f(NULL) = ∞
NULL-extended numerical preference constructors
Analogous to the NULL-extended categorical preference constructors, the numerical preference constructors are equipped with a NULL-handling parameter, too. Formally we define the numerical preference
P = C_d(A,X,≅_P,N)
with a preference constructor C, an attribute A, a SV-Relation, an optional d-parameter and parameters X (AROUND-value, BETWEEN-values, etc.), where the NULL-handling parameter N can take one of the following values:
- N_? means that NULL is incomparable to all other values, hence occurs in the preference's BMO-set. Analogous to categorical preferences, numerical base preferences loose their weak ordering if NULL values are specified to be incomparable to all other values.
- N^dist_v places NULL at the distance v to the preference's optimal values.
- N^level_v places NULL on level v (only applicable if a d-parameter is greater 0 and regular SV-semantics are used).
- N^dist_∞ specifies that NULL values are worse than all other ordinary values in the attribute domain.
NULL-extended complex preferences
Due to the NULL-extended categorical and numerical preference constructors, NULL values are now part of the preference order and the preferences are still strict partial orders. Therefore the composition of complex preferences can be applied straight forward to preferences based on the NULL-extended domain.
NULL-extended SV-semantics
For trivial SV-semantics x =_P x holds, whereas x =_P y is false in case x ≠ P_y This implies that NULL =_P NULL is always true in contrast to the standard SQL three-valued logic which would result in unknown.
For regular SV-semantics NULL becomes substitutable with all values v having the same level or the same distance to the preference's optimal values. If NULL is specified to be incomparable, it is not substitutable with any other domain value.
NULL-extended grouping preference
The preference P grouping A where A may be a single or multiple row value constructor elements (e.g. attributes), evaluates the preference P for all groups with the same value(s) for A separately. As part of the NULL-extension of Preference SQL, grouped preferences are also extended to handle NULL values. Naturally for the preference P grouping A groups containing NULL values for one of the row value constructor elements in A are also considered. To avoid this, the grouped preference P grouping¬N A only considers a group having a NULL value in one of the row value constructor elements in A, if the corresponding row value constructor element solely contains NULL values.
To make things a bit clearer, we first assume a grouped preference on a single attribute. For such a preference, a NULL-group is only taken into account if the grouping attribute contains only NULL values, otherwise it is discarded. Now let us look at a grouped preference on multiple attributes for which NULL values should be avoided. In this setting, a group containing a NULL value in at least one of the grouping attributes in only considered if all the attributes, for which the group is NULL, have only NULL values. As soon as one of these attributes contains other values than NULL, the group in not evaluated.
NULL-extended Preference SQL syntax
The previous section introduced a formal framework for handling NULL values in preferences and now we will look at the extended Preference SQL syntax capable of handling NULL values.
NULL-handling term for base preference constructors
For the placement of NULL values generally the following syntax is utilized:
[attribute][constructor][parameters][NULL−handling]
The first three parts of the term are well known and interpreted as usual. They correspond the the formal preference definition P = C_d(A,X,≅_P) already introduced in the preceding paragraph, however without d-parameter for categorical preferences. If the optional NULL-handling term is used, formally a preference P = C_d(A,X,≅_P,N) arises where N may take one of the previously presented values (see NULL-extended categorical preference constructors and NULL-extended numerical preference constructors).
Translated into Preference SQL syntax, the NULL-handling term may take one of the following forms:
- WITH NULL AT BMO: NULL is incomparable, i.e. N = N?. Consequently NULL always occurs in the preference's BMO-set, since incomparable attribute values do not dominate and are not dominated by any other value. Again, the statement WITH NULL AT BMO breaches a base preference's weak order that in turn influences the applicability of algorithms for preference evaluation.
- WITH NULL AT DISTANCE v: NULL is placed at the distance v from the preference's optimal values, i.e. N = N^dist_v. Note that this statement can only be applied to numerical preferences since it is not able to calculate a distance for categorical preferences.
- AVOID NULL: NULL becomes least preferred. Hence, every other available attribute value is rated better and NULL only occurs in the preference's BMO-set if there is nothing better at hand. The statement corresponds to the algebraic value N∞ for categorical preferences and N^dist_∞ for numerical preferences.
- WITH NULL AT LEVEL v: NULL is placed at the level v, i.e. N = N^level_v for numerical preferences and N = N_v for categorical preferences. Note that this statement requires that regular SV-semantics are used and for numerical preferences a d-parameter greater 0 has to be defined.
- WITH NULL WORST: NULL is placed at the same distance or level as the worst values of the preference's attribute domain, i.e. N takes on the value N^dist_max or N^level_max (if regular SV-semantics and a d-parameter greater 0 are used) for numerical preferences and N_max for categorical preferences. If the NULL-handling term is omitted in the definition of a preference, NULL values are placed among the worst attribute values by default. Hence, behind the scenes the statement WITH NULL WORST is assumed.
|
<NULL-handling> ::= AVOID NULL | WITH NULL WORST | WITH NULL AT BMO | WITH NULL AT DISTANCE <number> | WITH NULL AT LEVEL <number> |
NULL-extended categorical preference constructors
For categorical preference constructors there is another possibility to place NULL values in the preference order besides the previously presented NULL-handling statements. The NULL-extended Preference SQL syntax allows to include NULL values in the definition of layers. Since this is nothing surprising, the following listing just outlines the extended syntax for categorical preference constructors without any further explanation as it does not change the nature of a typical categorical preference in Preference SQL.
|
|
<column> { = { <string-literal> | <number> } | IS NULL | IN ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } [SV-relation] [NULL-handling] |
|
|
<column> { { != | <> } { <string-literal> | <number> } | IS NOT NULL | NOT IN ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } [SV-relation] [NULL-handling] |
|
|
<column> IN ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) ELSE ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) [SV-relation] [NULL-handling] |
|
|
<column> IN ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) NOT IN ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) [SV-relation] [NULL-handling] |
|
|
<column> LAYERED ( { ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) | OTHERS | { ( OTHERS, NULL ) | ( NULL, OTHERS ) } } [, { ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) | OTHERS | { ( OTHERS, NULL ) | ( NULL, OTHERS ) } } ] ) [SV-relation] [NULL-handling] |
Keep in mind that the current Preference SQL implementation does not lead to an error if NULL is placed in a POS-set, NEG-set or layer and additionally a NULL-handling statement is given. In this case, positioning NULL in a POS-set, NEG-set or layer takes precedence over any potentially specified NULL-handling term, i.e. the NULL-handling term is not taken into account for preference evaluation.
NULL-extended explicit preference
NULL can now be used to construct the better-than graph of an explicit preference, too. Thus the syntax for an explicit preference was adapted in order to be able to include NULL in the definition of the ordered pairs determining the better-than graph.
|
<column> EXPLICIT ( { <string-literal> | NULL |( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } < { <string-literal> | NULL | ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } [, { <string-literal> | NULL |( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } < { <string-literal> | NULL |( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) } ]* ) |
NULL-extended explicit SV-relation
Of course, besides the usage of NULL in the definition of layers and explicit preferences, it is now possible to apply them in an explicit SV-relation, too. Consequently the SV-relation term now looks like the following:
|
<SV-relation> ::= { REGULAR | TRIVIAL | SV ( { ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) | OTHERS } [, ( { <string-literal> | <number> | NULL } [, <string-literal> | <number> | NULL]* ) | OTHERS ]*) } |
NULL-extended grouping preference
To avoid NULL values for a row value construtor element in a grouped preference, i.e. formally to define a preference P grouping¬N A, the statement AVOID NULL is placed after the desired row value constructor element. In order to facilitate the definition of AVOID NULL for several row value constructor elements, these can be enclosed in brackets followed by the statement AVOID NULL.
If a row value constructor element is equipped with the AVOID NULL statement, a group containing a NULL value in this element will only be considered if the element contains nothing else than NULL values. Otherwise this group is discarded. The same holds for more than one row value constructor element defined to avoid NULL-groups. If for at least one row value constructor element exist other values than NULL, a group containing a NULL value in the corresponding row value constructor element is omitted. But if a row value constructor element is not specified to avoid a NULL-group, it does not affect the selection of groups to be evaluated by the preference.
The extension of a grouped preference to handle NULL values or rather to avoid NULL values, leads to the following syntax in Preference SQL:
|
<GROUPING- clause> ::= { <row-value-constructor-element> [ <GROUPING- SV-relation>] [AVOID NULL] | ( <row-value-constructor-element> [ <GROUPING- SV-relation>] [, <row-value-constructor-element> [ <GROUPING- SV-relation>]]* ) [AVOID NULL] } [, <row-value-constructor-element> [ <GROUPING- SV-relation>] [AVOID NULL] | ( <row-value-constructor-element> [ <GROUPING- SV-relation>] [, <row-value-constructor-element> [ <GROUPING- SV-relation>]]* ) [AVOID NULL] ]* |
Syntactical limitations
Regarding the NULL-handling WITH NULL AT BMO there are some limitations at the moment. As already described the statement WITH NULL AT BMO places NULL values in a base preference's BMO-set, i.e. NULL is as good as the best attribute values. Unfortunately the current NULL-extension implementation does not allow its usage for the definition of a score preference as part of a rank preference. Moreover the LEVEL() function cannot be utilized in case the base preference uses the statement WITH NULL AT BMO or one of the constituent parts of a complex preference uses it. Currently in both cases an error is raised. These shortcomings arise from the fact that a base preference's weak ordering is breached by specifying NULL values as incomparable.
The section Implementation dependent limitations clarifies in more detail why this is not possible at the moment from the point of view of implementation and the section Future work proposes an approach to overcome these shortcomings.
Example use cases
For many scenarios each of the presented NULL-handling strategies can be mapped to a user type. Revisiting the scenario from the Introduction we can identify the following user types:
- Experienced user: The experience user might know a lot of hiking tours by heart. Hence, he wants to substitute unknown values with concrete values from his experience.
- Indifferent user: He does not care about the functionality of a database system and does not know what unknown values are. He just wants to obtain the best matching tours regarding his preferences.
- Cautious user: He wants to plan his hiking tour in all details. He prefers tours for which all information is available to make a conscious decision. Consequently, the last thing he wants are unknown values.
- Adventurous user: He wants to tackle new challenges and is ready to complete missing tour information with his own experience. Hence, he is indifferent concerning fully documented tours and tours with missing information.
Experienced user
An experienced user might know that the average tour length within the desired area is about 35 kilometers and that tours with unknown difficulty are rarely really difficult ones. Let us say the experienced user generally prefers tours of around 50 kilometers and a hard difficulty level. Hence, the query posed looks as follows:
|
SELECT * FROM hiking_tour PREFERRING length AROUND 50 WITH NULL AT DISTANCE 15 AND difficulty IN ('hard') WITH NULL AT LEVEL 1; |
The experienced user sets an explicit distance of 15 to use for NULL values, since he knows the average tour length is 35 kilometers. As a result he obtains the following tuples:
| id | length | difficulty | rating | visa |
| 2 | NULL | easy | 5 | bad |
| 3 | NULL | NULL | 2 | bad |
| 4 | 13.1 | hard | 2 | good |
Indifferent user
An indifferent user might prefer tours with excellent vista and lowest tour length, thus he poses the following query:
|
SELECT * FROM hiking_tour PREFERRING vista IN ('excellent') AND length LOWEST; |
Since he does not know much about NULL values, he does not specify an explicit NULL-handling term. Hence, the default behavior is in place which treats NULL values as good as the worst values in the attribute domain, i.e. the NULL-handling statement WITH NULL WORST is used. As a result he obtains the subsequent tuples:
| id | length | difficulty | rating | vista |
| 5 | 7.3 | NULL | 1 | excellent |
Cautious user
A cautious user might look for hiking tours that are very easy and thus poses the following Preference SQL query:
|
SELECT * FROM hiking_tour PREFERRING difficulty IN ('very easy') AVOID NULL; |
He chooses to avoid NULL values in the difficulty attribute, i.e. NULL values are rated worse than any other available attribute value. As a result he obtains the following tuples:
| id | length | difficulty | rating | vista |
| 1 | 23.5 | medium | 4 | excellent |
| 2 | NULL | easy | 5 | bad |
| 4 | 13.1 | hard | 2 | good |
There are no perfect matches for his preferred difficulty of very easy, but as desired he did not receive any NULL value in the difficulty attribute. Hence, the best alternatives that do not contain NULL in the difficulty attribute are returned.
Adventurous user
An adventurous user might like hiking tours whose length is between 15 and 20 kilometers with a tolerance of 5 kilometers. With a lower priority he might also be interested in a medium difficulty.
|
SELECT * FROM hiking_tour PREFERRING length BETWEEN 15 AND 20, 5 WITH NULL AT BMO PRIOR TO difficulty IN ('medium') WITH NULL AT BMO; |
He specifies NULL to be a best match for each base preference and thus gets the following tuples:
| id | length | difficulty | rating | vista |
| 1 | 23.5 | medium | 4 | excellent |
| 3 | NULL | NULL | 2 | bad |
References
- Handling of NULL Values in Preference Database Queries - M. Endres, P. Roocks, F. Wenzel, A. Huhn, W. Kießling (2012)